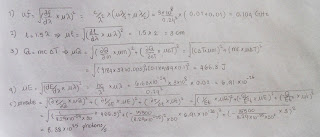Introduction
The purpose of this experiment
was to understand the standing waves created by electromagnetic waves, to solve
the possible dimensions for microwaves by using standing waves concept, and to
compute the rate of oscillating photons and the pressure exerted on the walls of
microwaves by these photons.
This
experiment was conducted using a microwave, a bag of marshmallows, a paper, a
cup of 100g of water, and a multimeter. Marshmallows were uniformly spread out
on a paper and were microwaved for a few seconds to observe the standing wave
pattern created by the electromagnetic waves. Half of the wavelength was
obtained by measuring crest to crest of the marshmallows. The dimensions of the
microwave were also recorded. Then 100 g of water was microwaved for 30s, and
the change in temperature was recorded. The frequency and the dimensions of the
microwave were computed by using the measured half wavelength. Also, the total
energy content, the rate of photons oscillating in the microwave, and the
pressure exerted by these photons on each dimension of the microwave were
computed by using the concepts of heat transfer, Planck relation, and energy
and momentum in electromagnetic waves. The following equations describing these
concepts were used.
Heat
transfer: Q=mc∆T (1)
Planck
Relation: E=hc/λ (2)
Energy and
Momentum in electromagnetic waves: I=P/A=pradc (3)
Figure 1: Marshmallows before being microwaved
Figure 2: Measuring water temperature after microwaving for 30s
Video 1: Microwaving marshmallows: Marshmallows formed 3-dimensional standing waves pattern as it was being microwaved.
Data and
Analysis
Table-1: Various recorded
and calculated values from this experiment
Experimental
measurements
|
Calculated values
|
|||
λ/2(cm)
|
12.0 ± 1.0
|
ƒ(GHz)
|
1.25 ± 0.104
|
|
Length(cm)
|
35.0 ± 1.0
|
Length(cm)
|
36 ± 3.0
|
|
Width(cm)
|
35.0 ± 1.0
|
Width(cm)
|
36 ± 3.0
|
|
Height(cm)
|
23.0 ± 1.0
|
Height(cm)
|
20.0 ± 2.0
|
|
Amplitude(cm)
|
10.0 ± 1.0
|
Q(J)
|
15500 ± 466
|
|
Masswater(g)
|
100.0 ± 3.0
|
Ephotons(J)
|
(8.29 ± 0.691)x10-25
|
|
Tempi(˚C)
|
20.0 ± 0.05
|
Rate(photons/s)
|
(6.23 ± 0.833)x1026
|
|
Tempi(˚C)
|
57.0 ± 0.05
|
Power(W)
|
516 ± 54
|
|
Time(s)
|
30.0 ± 3.0
|
pphotons(μPa)
|
35x35
|
14.0 ± 2.72
|
35x23
|
21.4 ± 5.77
|
|||
In this experiment, the
wavelength of the standing waves created by microwave was considered to be 24cm
since the length from crest to crest of the marshmallows shown in figure 3 were
12cm apart. According to table 1, the computed dimensions of the microwave were
36x36x20 which were within the uncertainties of the measured values 35x35x23.
The computed length and width of the microwave were greater than that of the
measured values. This was because it was assumed that in each dimension of the
paper, there was one and a half wave. In fact, as shown in figure 3, there was
less than one and a half wave. Hence, the possible length and width should have
been smaller than 36x36. In addition, the amplitude of the standing wave was
measured to be 10cm which was a half of the height of the microwave. Therefore,
the height was considered to be 20cm, but it was only an approximation.
Therefore, it had a large uncertainty. If the height could not be approximated,
the height of the microwave could possibly be any height approximately equal to
or greater than 10cm in this particular case. If it was a lot lower than 10cm,
standing waves will not possible be observed due to compression on marshmallows
by the height limit.
According to table 1, the
frequency of the standing microwave was 1.25GHz, and it was computed by using
the relationship between the speed of light, the frequency, and the measured
wavelength. The result was within the normal range, 1-300GHz*, of the frequency
emitted from a microwave oven. Besides, the heat content which was 15500J was also
computed by using the measured mass and the temperature change of 100g of water.
Moreover, computation revealed that there were (6.23 ± 0.833)x1026
photons oscillating in the microwave in a second. These photons exerted 14 to
21.4 μPa on each
wall of the microwaves. This result was obtained by using equation 3 described
in the introduction. Lastly, the power of the microwave was experimentally
calculated to be 516W, which agreed with the power produced by a typical
consumer microwave ranging from 400W to 1200W*.
*source: Frequency of a Microwave, Power of a Microwave